Duck Chase

Imagine our yellow dot is a duck swimming in a pond, and the red dot is a hungry fox. The fox circles around the pond to search for an opportunity to catch the duck. The duck is safe in the pond, but it needs to reach the shore to escape.

Game Rules

1. Click anywhere on the canvas to move the duck to the pointed location.
2. The fox (red) will chase the duck, such that it minimizes its distance to the duck.
3. If the duck reaches the shore without being caught, then you win!

Turn around and run?

Intuitively, we may be tempted to run in the opposite direction of the fox and take the shortest path ashore. But the speed of the fox is set up to be at least $\pi$ times the duck's speed. Therefore, as the duck moves towards the shore, the fox will surely catch up.

Solution

Step One

As you probably noticed, if the duck moves along or outside the grey circle, it will maintain the same angle with the fox. This is because beyond the grey circle, the angular velocity of the duck is the same as the fox: $\omega_{duck} = \omega_{fox}$.

On the flip side, if the duck moves within the grey circle, it can potentially increase its angle difference with the fox. This gives us an idea for a strategy: move spirally towards the grey circle from the center of the pond.

This way, the duck can gradually increase its angle difference with the fox. In an ideal scenario, the duck can reach a point on the grey circle that is at most $\pi$ or $180^\circ$ away from the fox, marking the maximum angle and distance away from the fox.

Step Two

Maybe take the shortest path now?

Intuitively, we may think from this optimal point, the duck should take the shortest path to the shore. But is this really the best strategy?

Well, if you give it a try, you may find as we increase the speed of the fox, this strategy may not work as well.

Optimize it!

Assuming we followed step one, and we are at the optimal point (maximum angle/distance away from the fox), as shown in the graph below. We can then formulate this problem of finding the optimal path from this point onwards into an optimization.

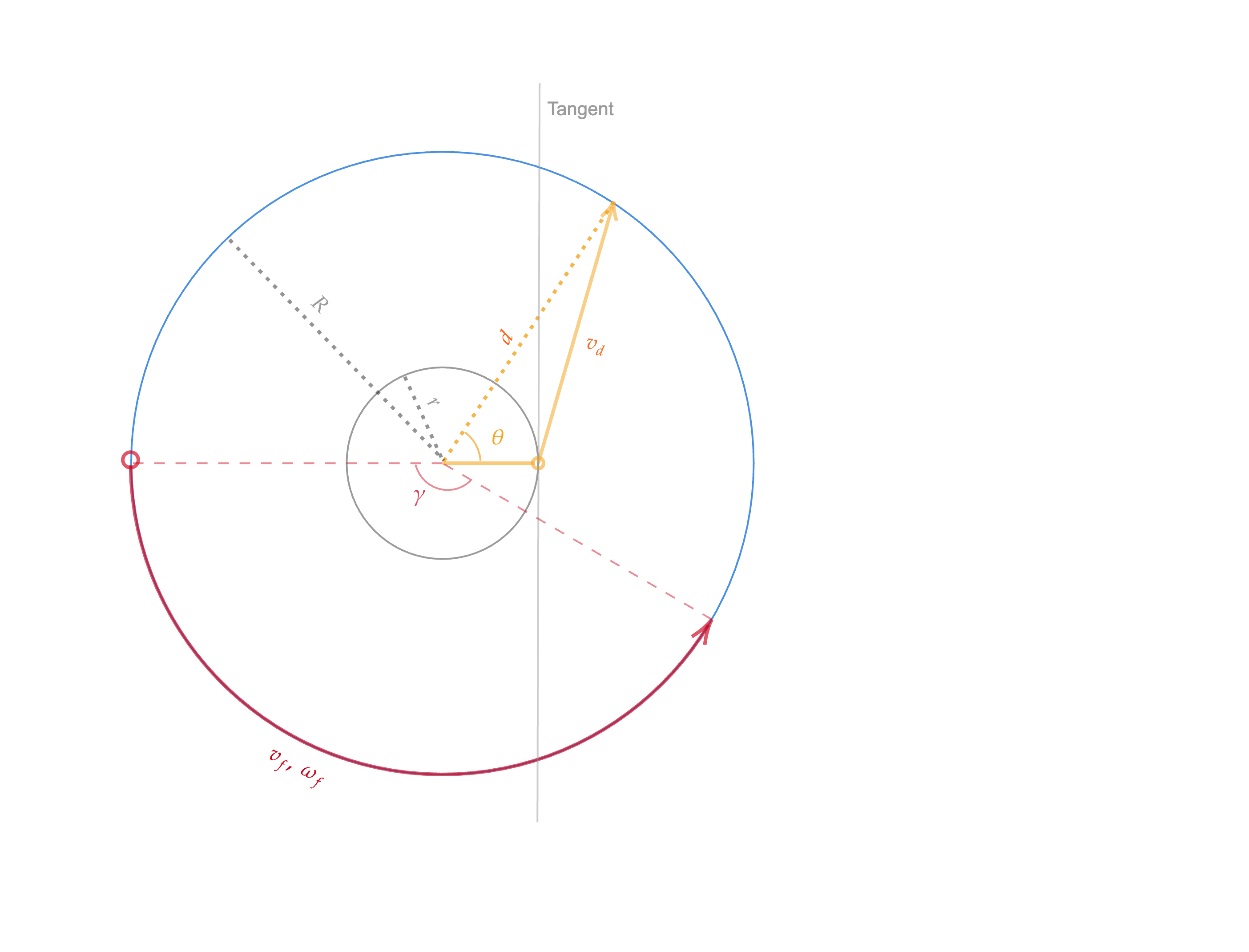
As shown in the plot, we will first define a few variables:

• $v_d$ to be the duck's velocity, $v_f$ to be the fox's velocity, and $\omega_f$ to be its angular velocity.
• $r$ to be the grey circle's radius, $R$ to be the pond's radius.
• $\theta$ to be the potential angle the duck takes to reach the shore, while $\gamma$ is the angle the fox will travel during the time the duck takes to reach the shore.
• $d$ being the distance the duck travels.

From here, we can immediately derive a few relations:

1. $\frac{r}{R} = \frac{v_d}{v_f}$
2. $d = \sqrt{(R \cos{\theta} - r)^2 + (R\sin{\theta})^2} = \sqrt{R^2 + r^2 - 2Rr\cos{\theta}}$
3. $\gamma = \frac{d}{v_d}\omega_f = \frac{d}{v_d}\frac{v_f}{R} = \frac{d}{r}$

We will define the objective as the final angle between the duck and fox and aim to maximize it: $$f(\theta) = \theta + \pi - \gamma = \theta + \pi - \frac{\sqrt{R^2 + r^2 - 2Rr\cos\theta}}{r}, \text{where } 0\leq\theta\leq \arccos{\frac{r}{R}}.$$

Side note on the limits: if $\theta\lt 0$, then it will certainly be worse for the duck as it travels in the direction of the fox. If $\theta\gt \arccos{\frac{r}{R}}$, which means the duck travels beyond the tangent line, this will cause the fox to chase in the opposite direction, resulting in a speedier catch/failure as well.

We can take derivative and attempt to solve for optimal solution (assume there is one). $$f'(\theta) = 1 - \frac{R\sin\theta}{\sqrt{R^2 + r^2 - 2Rr\cos\theta}} = 0$$ With basic calculus, we get the following, $$R^2\cos^2\theta - 2Rr\cos\theta + r^2 = 0$$ $$\theta = \arccos{\frac{r}{R}}$$ This means our upper limit for $\theta$ (intersection of the tangent line to the grey circle and the pond) happens to be a critical point.

To further confirm, we can also plot out the solution for the case when $v_f = \pi v_d$.

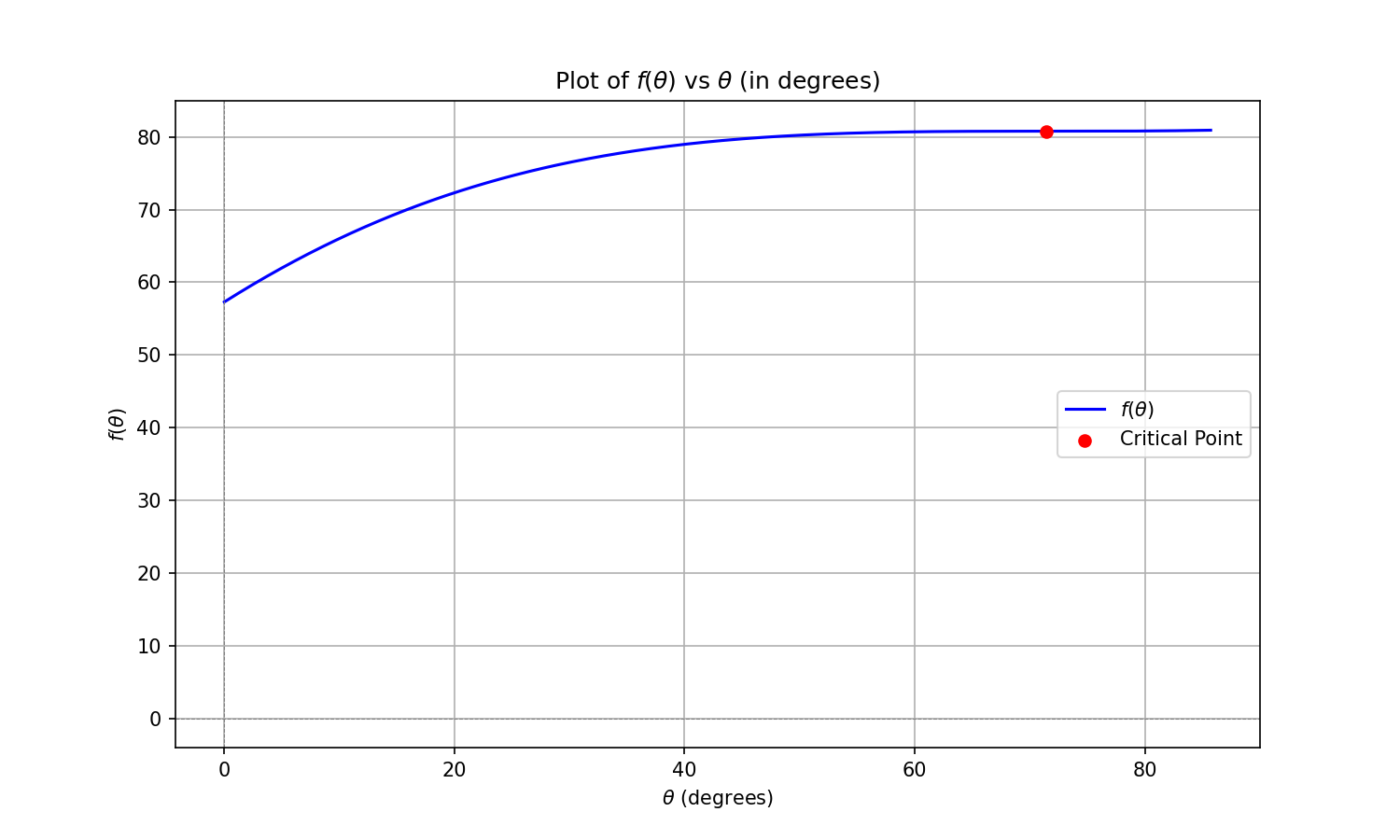
The optimal path onwards is indeed to aim for an angle of $\theta = \arccos{\frac{r}{R}}$.

Conclusion

The optimal strategy is as follows:

1. Move spirally towards the grey circle from the center of the pond, until the duck reaches maximum angle/distance away from the fox.
2. From that point, move along the tangent line of the grey circle to the shore.

Give it a try!