Duck and Fox

Imagine a duck swimming in a circular pond, and a fox circling around the edge. The fox is faster, but the duck is safe in the water. The duck needs to reach the shore to escape.

Try the interactive game →

Rules

  1. Click anywhere on the canvas to move the duck to that location
  2. The fox (red) chases the duck, minimizing its distance to the duck
  3. If the duck reaches the shore without being caught, you win!

Turn around and run?

Intuitively, we may be tempted to run in the opposite direction of the fox and take the shortest path ashore. But the speed of the fox is set up to be at least $\pi$ times the duck's speed. Therefore, as the duck moves towards the shore, the fox will surely catch up.

Solution

Hint: Try moving along the grey circle within the pond.

Step One

If the duck moves along or outside the grey circle, it maintains the same angle with the fox. This is because beyond the grey circle, the angular velocity of the duck equals that of the fox: $\omega_{duck} = \omega_{fox}$.

If the duck moves within the grey circle, it can increase its angular difference with the fox. This gives us a strategy: move spirally towards the grey circle from the center of the pond.

This way, the duck can gradually increase its angular difference with the fox. In an ideal scenario, the duck can reach a point on the grey circle that is $\pi$ (or $180^\circ$) away from the fox — the maximum possible distance.

Step Two

Maybe take the shortest path now?

From this optimal point, should the duck take the shortest path to the shore? If you try it, you'll find that as we increase the fox's speed, this strategy may not work.

Optimization

Assuming we followed step one and are at the optimal point (maximum angle/distance from the fox), as shown below, we can formulate this as an optimization problem.

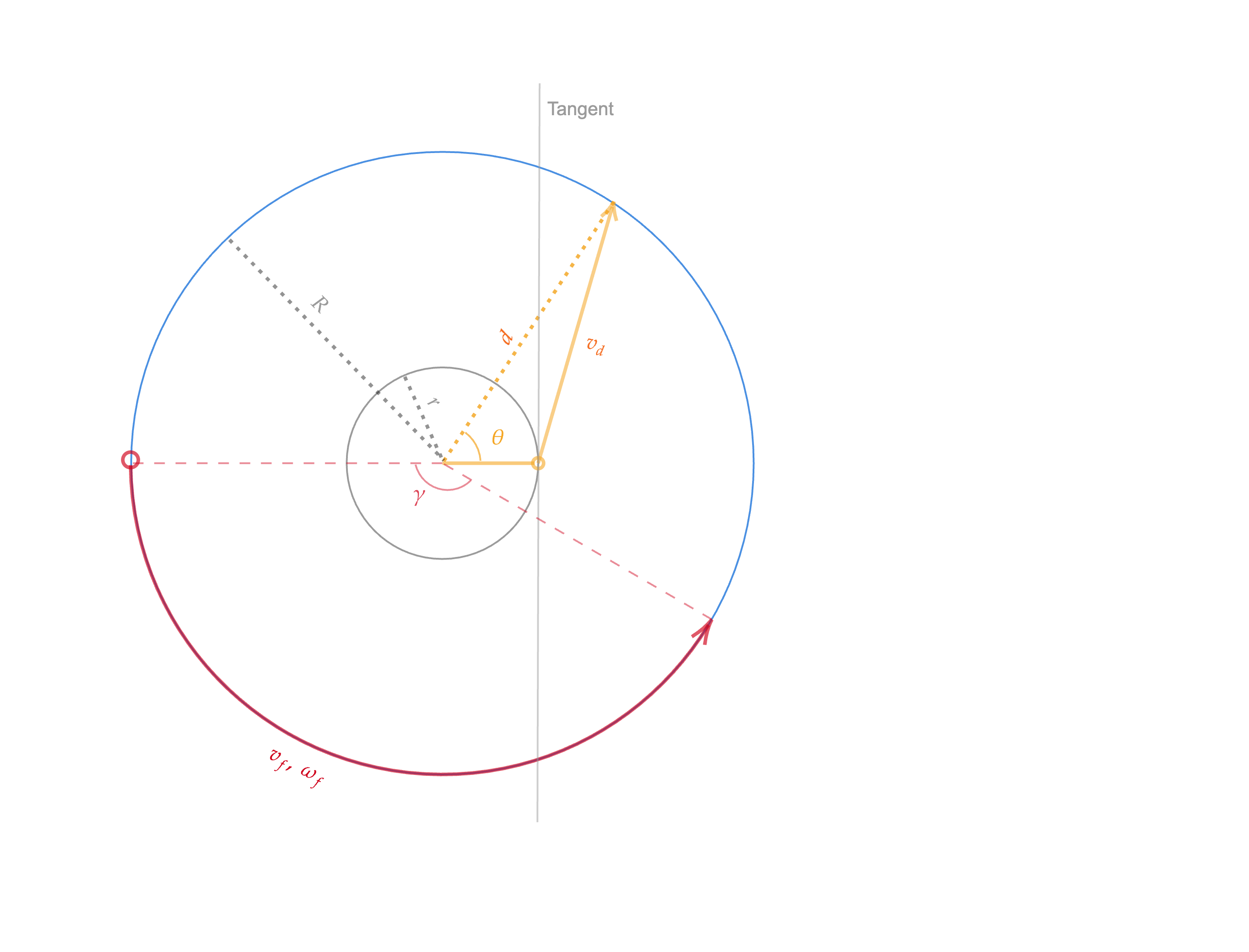
optimal_scenario

Define the following variables:

  • $v_d$: duck's velocity, $v_f$: fox's velocity, $\omega_f$: fox's angular velocity
  • $r$: grey circle's radius, $R$: pond's radius
  • $\theta$: angle the duck takes to reach the shore
  • $\gamma$: angle the fox travels while the duck reaches the shore
  • $d$: distance the duck travels

From here, we derive:

  1. $\frac{r}{R} = \frac{v_d}{v_f}$
  2. $d = \sqrt{(R \cos{\theta} - r)^2 + (R\sin{\theta})^2} = \sqrt{R^2 + r^2 - 2Rr\cos{\theta}}$
  3. $\gamma = \frac{d}{v_d}\omega_f = \frac{d}{v_d}\frac{v_f}{R} = \frac{d}{r}$

The objective is to maximize the final angle between duck and fox:

$$f(\theta) = \theta + \pi - \gamma = \theta + \pi - \frac{\sqrt{R^2 + r^2 - 2Rr\cos\theta}}{r}, \text{ where } 0 \leq \theta \leq \arccos{\frac{r}{R}}$$

Note on limits: if $\theta < 0$, the duck travels toward the fox. If $\theta > \arccos{\frac{r}{R}}$ (beyond the tangent line), the fox reverses direction, catching the duck faster.

Taking the derivative and solving:

$$f'(\theta) = 1 - \frac{R\sin\theta}{\sqrt{R^2 + r^2 - 2Rr\cos\theta}} = 0$$

With basic calculus:

$$R^2\cos^2\theta - 2Rr\cos\theta + r^2 = 0$$ $$\theta = \arccos{\frac{r}{R}}$$

The upper limit for $\theta$ (tangent line intersection) is also the critical point.

Plotting the solution for $v_f = \pi v_d$:

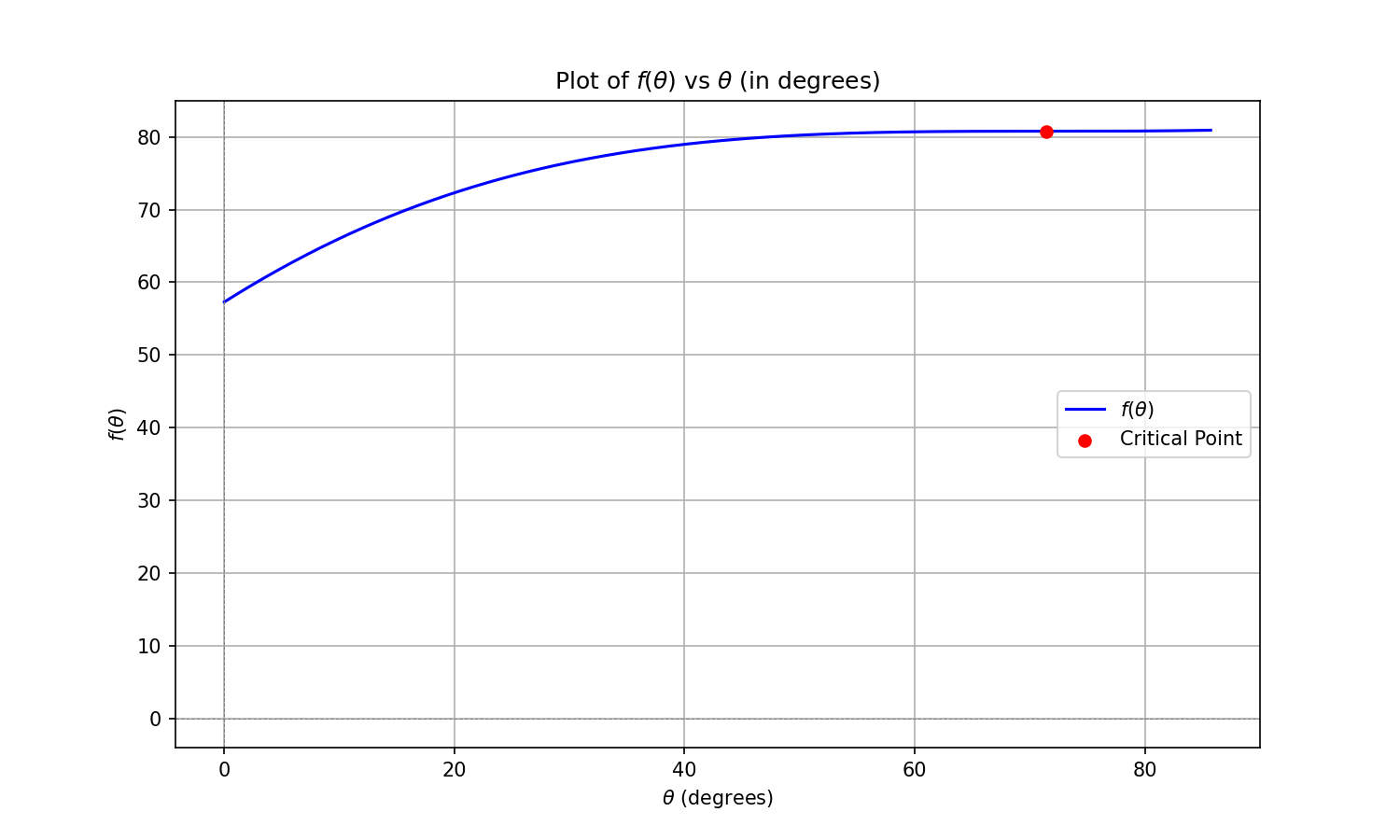
solution

The optimal path is to aim for angle $\theta = \arccos{\frac{r}{R}}$.

Conclusion

The optimal strategy:

  1. Move spirally towards the grey circle from the center, until reaching maximum angular distance from the fox
  2. From that point, move along the tangent line to the shore